数据结构-二叉树

二叉树

二叉树是n（n >= 0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成

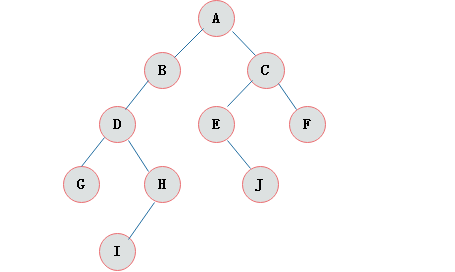
二叉树的特点

1. 每个结点最多有两颗子树，所以二叉树不存在度大于2的结点

2. 左子树和右子树是有顺序的，次序不能颠倒

3. 即使树中某结点只有一颗子树，也要区分它是左子树还是右子树

二叉树的数据结构

由于二叉树最多有两个孩子，所以我们可以创建拥有一个数据域和两个指针域的结构体，由这些结构体构成的链表也叫二叉链表

typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BitNode, *BiTree;

二叉树遍历

前序遍历

若二叉树为空，则返回，否则先访问根结点，然后前序遍历左子树，再遍历右子树

void PreOrederTraverse(BiTree T)
{
    if (T == NULL)
    {
        return;
    }
    printf("%c",T->data);
    PreOrederTraverse(T->lchild);
    PreOrederTraverse(T->rchild);
}

中序遍历

若二叉树为空，则返回，否则按照左子树，根结点，右子树的顺序遍历

void InOrederTraverse(BiTree T)
{
    if (T == NULL)
    {
        return;
    }
    InOrederTraverse(T->lchild);
    printf("%c",T->data);
    InOrederTraverse(T->rchild);
}

后序遍历

若二叉树为空，则返回，否则按照左子树，右子树，根结点的顺序遍历

void PostOrederTraverse(BiTree T)
{
    if (T == NULL)
    {
        return;
    }
    PostOrederTraverse(T->lchild);
    PostOrederTraverse(T->rchild);
    printf("%c",T->data);
}

创建二叉树

以#代表空结点,使用前序创建二叉树

void PreCreateBiTree(BiTree *T)
{
    char ch;
    scanf("%c",&ch);
    if (ch == '#')
    {
        *T = NULL;
    }
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        if (!*T)
        {
            exit();
        }
        (*T)->data = ch;
        PreCreateBiTree(&(*T)->lchild);
        PreCreateBiTree(&(*T)->rchild);
    }
}

只实现了前序创建，中序和后序创建有点问题，目前不知道哪里出现了错误